第4章:微分方程的应用
第四章:微分方程的应用 -- 建模的艺术¶
如果说前三章我们学习的是微分方程的“招式”,那么这一章我们就来见识一下它的“威力”! 前面那些看似枯燥的公式和解法,一旦与实际问题结合起来,就会立刻变得鲜活生动,展现出强大的力量。
微分方程就像一位技艺精湛的雕塑家,能够将现实世界中各种纷繁复杂的现象,雕琢成一个个简洁而优美的数学模型。 通过这些模型,我们可以洞察事物的本质,预测未来的走向,甚至控制系统的行为。
在本章中,我们将一起踏上这段奇妙的旅程,看看微分方程是如何在各个领域大显身手的!
4.1 人口增长模型 -- 指数的力量¶
让我们从一个经典的问题开始:人口增长。
早在 18 世纪末,英国牧师马尔萨斯就提出了一个著名的人口增长模型。 他认为,在资源充足的条件下,人口的增长速度与当时的人口数量成正比。 换句话说,人口越多,增长得就越快。
这个想法很符合直觉,让我们用微分方程来描述它。 设 \(P(t)\) 表示 \(t\) 时刻的人口数量,那么人口的增长速度就是 \(\frac{dP}{dt}\)。 根据马尔萨斯的假设,我们有:
其中 \(r\) 是一个常数,表示人口的自然增长率。
这个微分方程我们在前面已经见过,它是一个简单的一阶线性微分方程,而且是可分离变量的。 它的解是:
其中 \(P_0 = P(0)\) 表示初始时刻的人口数量。
这个解告诉我们,在马尔萨斯的模型下,人口数量将以指数形式增长! 这就是著名的 马尔萨斯人口模型,也称为 指数增长模型。
指数增长是一种非常惊人的增长模式。 让我们想象一下:假如你有一张足够大的纸,对折一次,厚度变成原来的 2 倍;再对折一次,厚度变成原来的 4 倍…… 如此反复,对折多少次后,纸的厚度可以超过地球到月球的距离呢? 答案可能让你大吃一惊:只需要大约 42 次! 这就是指数增长的威力。
当然,现实世界中,人口不可能永远按照指数形式增长。 随着人口数量的增加,资源会变得越来越稀缺,环境压力也会越来越大,人口的增长速度会逐渐放缓。 这就需要我们对马尔萨斯模型进行修正。
4.1.1 Logistic 模型 -- 有限的增长
为了更准确地描述人口增长,我们需要考虑资源和环境的限制。 一个更合理的假设是:人口的增长率 \(r\) 不是一个常数,而是随着人口数量 \(P\) 的增加而减小。
一种简单的假设是 \(r\) 与 \(P\) 呈线性关系:
其中 \(r_0\) 是初始增长率,\(a\) 是一个正的常数。 将这个关系代入人口增长方程,我们得到:
为了简化方程,我们令 \(K = \frac{r_0}{a}\),则方程变为:
这个方程叫做 Logistic 方程,也称为 阻滞增长模型。
\(K\) 的含义是什么呢? 当 \(P\) 接近 \(K\) 时,\(\frac{dP}{dt}\) 接近于 0,也就是说,人口数量趋于稳定。 因此,\(K\) 表示环境能够承载的最大人口数量,称为 环境容量。
Logistic 方程也是一个可分离变量的微分方程,我们可以求得它的解为:
这个解的图形是一条 S 形曲线,也称为 Logistic 曲线。
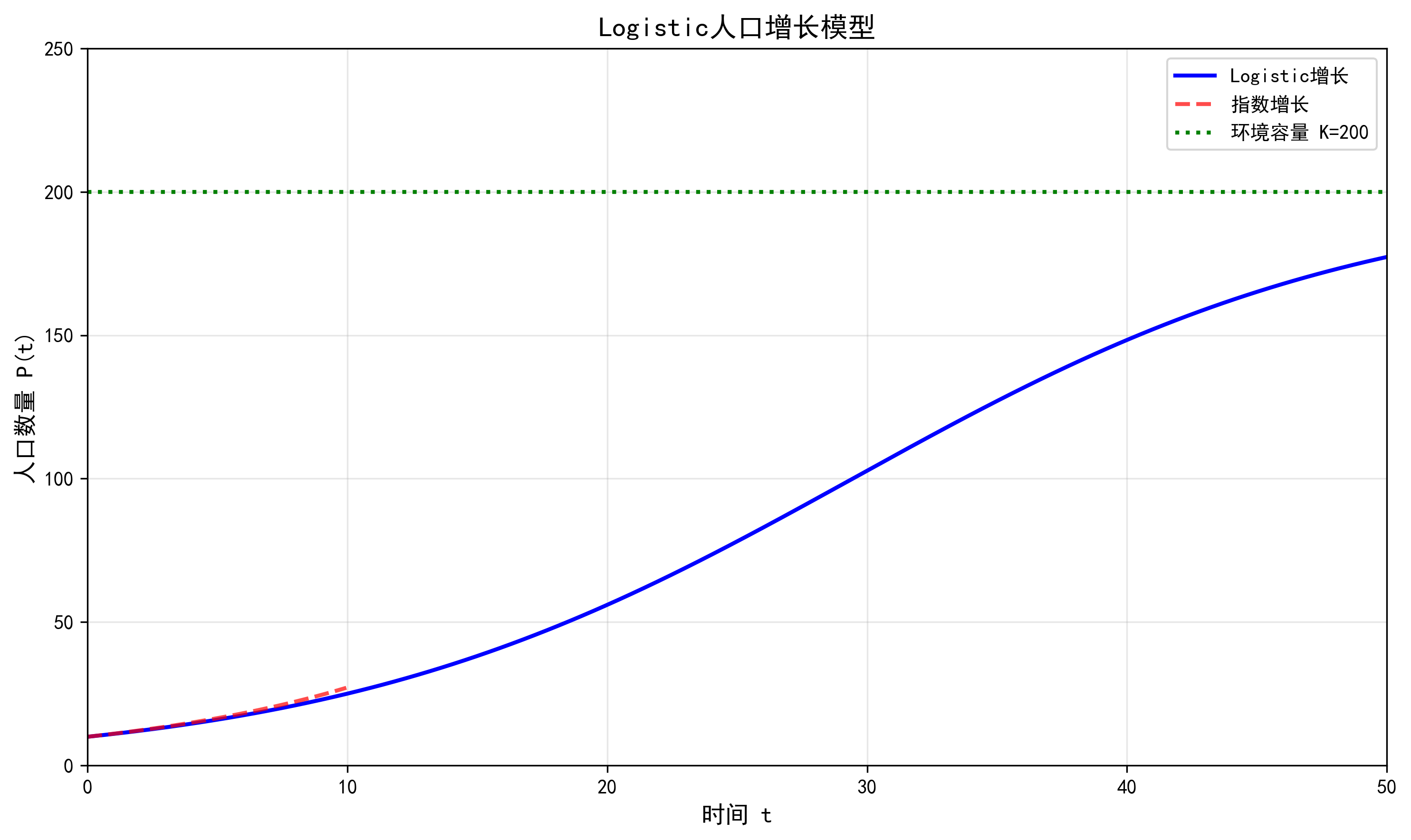
从图中我们可以看到,当 \(t\) 较小时,\(P(t)\) 接近于指数增长;随着 \(t\) 的增大,\(P(t)\) 的增长速度逐渐放缓,最终趋于稳定值 \(K\)。
Logistic 模型比马尔萨斯模型更符合实际情况,它成功地描述了许多生物种群的增长规律,也常用于预测市场饱和度、技术扩散等社会经济现象。
4.1.2 习题
- 假设世界人口的初始增长率为每年 2%,环境容量为 200 亿。如果世界人口在 1980 年为 45 亿,请使用 Logistic 模型预测 2023 年的世界人口数量,并与实际数据进行比较。
- Logistic 模型有哪些局限性? 请尝试提出一些改进的思路。
4.2 传染病模型 -- 信息的传播¶
微分方程不仅可以用来描述人口的增长,还可以用来描述疾病的传播。
在一个封闭的群体中,当一种传染病开始传播时,人群可以分为三类:
- 易感者 (Susceptible): 还没有感染疾病,但有可能被感染的人。
- 感染者 (Infected): 已经感染疾病,并能够传播疾病的人。
- 康复者 (Recovered): 已经康复,并对疾病具有免疫力的人。
我们分别用 \(S(t)\), \(I(t)\), \(R(t)\) 表示 \(t\) 时刻这三类人群的数量。
4.2.1 SI 模型 -- 最简单的传染病模型
我们先来看一个最简单的传染病模型,叫做 SI 模型。 这个模型假设:
- 人群总数 \(N\) 保持不变,即 \(S(t) + I(t) = N\)。
- 感染者不会康复,也不会死亡 (例如,某些慢性病)。
- 感染者的增长速度与易感者和感染者的接触机会成正比。
根据这些假设,我们可以得到如下的微分方程:
其中 \(\beta\) 是一个常数,表示传染率。
由于 \(S(t) = N - I(t)\),所以我们可以将方程改写为:
这个方程是不是很眼熟? 是的! 它和 Logistic 方程的形式非常相似!
实际上,如果我们令 \(I(t) = N - S(t)\),那么 SI 模型就变成了 Logistic 方程。
SI 模型的解也是一条 S 形曲线,它表明感染者数量最终将趋于总人口数 \(N\),也就是说,所有人最终都会被感染。
4.2.2 SIR 模型 -- 更接近现实的模型
SI 模型过于简单,它没有考虑康复者的存在。 一个更接近现实的模型是 SIR 模型。 SIR 模型假设:
- 人群总数 \(N\) 保持不变,即 \(S(t) + I(t) + R(t) = N\)。
- 感染者以一定的速率 \(\gamma\) 康复。
- 康复者获得免疫力,不再被感染。
根据这些假设,我们可以得到如下的微分方程组:
其中 \(\beta\) 是传染率,\(\gamma\) 是康复率。
SIR 模型没有简单的解析解,但我们可以通过数值方法 (例如欧拉方法) 来求解它。
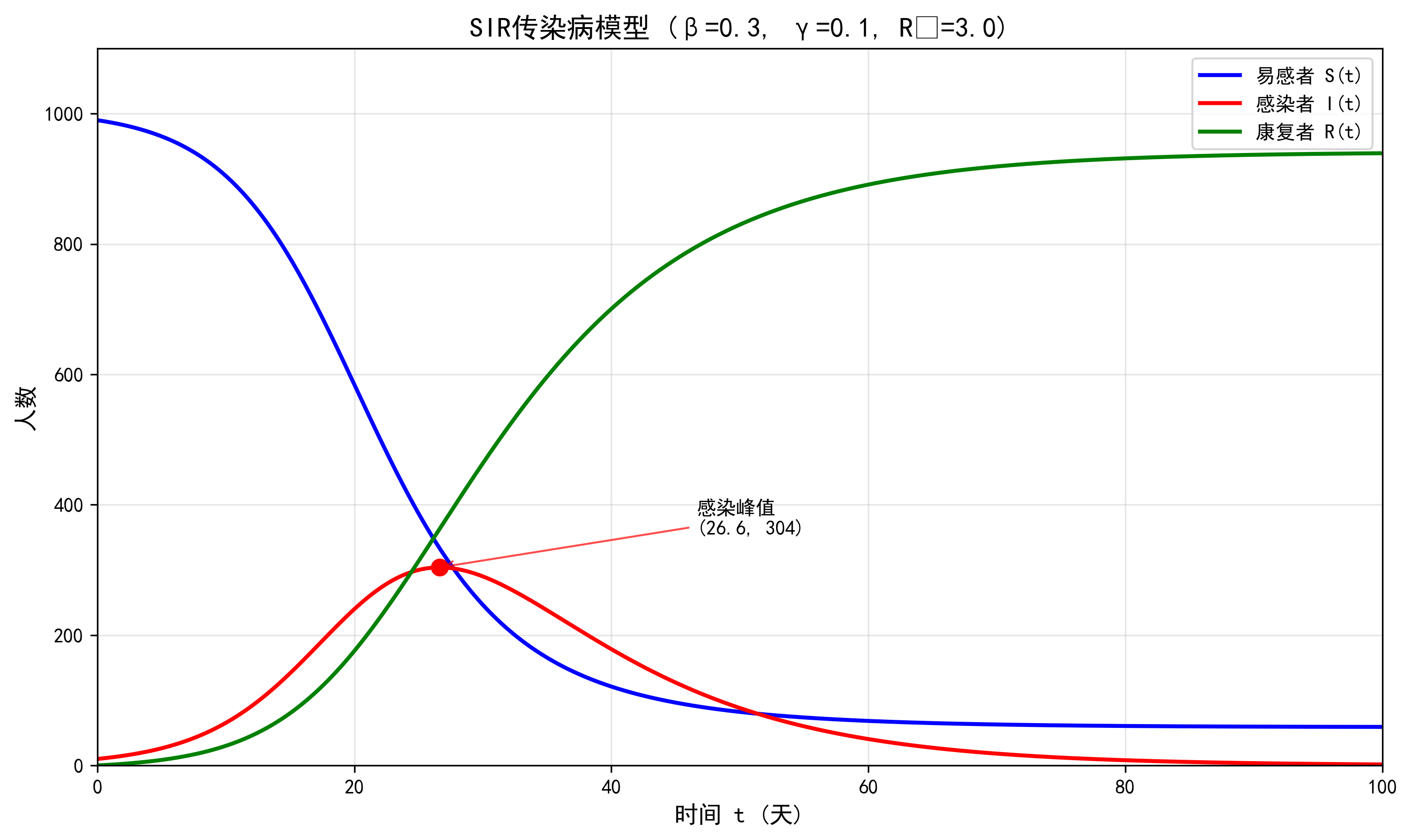
从图中我们可以看到,感染者数量 \(I(t)\) 先是上升,达到一个峰值,然后下降,最终趋于 0;而康复者数量 \(R(t)\) 则不断上升,最终趋于一个稳定值。
SIR 模型是传染病动力学中一个非常重要的模型,它被广泛应用于各种传染病的建模和预测,例如 SARS、COVID-19 等。
4.2.3 习题
- 解释 SIR 模型中参数 \(\beta\) 和 \(\gamma\) 的含义,以及它们对传染病传播的影响。
- 如果考虑死亡因素,SIR 模型应该如何修改?
- 请查阅资料,了解 SIR 模型的变种,例如 SEIR 模型、SIRS 模型等,并比较它们的异同。
4.3 牛顿冷却定律 -- 温度的秘密¶
物理学中也有许多微分方程的用武之地。 例如,牛顿冷却定律描述了物体温度的变化规律。
牛顿冷却定律指出:一个物体的温度变化速率与该物体和周围环境的温度差成正比。
设 \(T(t)\) 表示物体在 \(t\) 时刻的温度,\(T_a\) 表示周围环境的温度,那么牛顿冷却定律可以用如下的微分方程来表示:
其中 \(k\) 是一个正的常数,称为冷却系数。 负号表示当物体温度高于环境温度时,物体温度下降。
这个方程也是一个一阶线性微分方程,而且是可分离变量的。 它的解为:
其中 \(T_0 = T(0)\) 表示物体的初始温度。
这个解告诉我们,物体的温度将以指数形式趋近于周围环境的温度。
例 4.3.1 一杯热咖啡放在 20°C 的房间里。 1 分钟后,咖啡的温度从 80°C 降至 60°C。 问:咖啡的温度降至 40°C 需要多长时间?
解:
根据牛顿冷却定律,我们有:
将 \(t=1\),\(T=60\) 代入,得到:
解得 \(k = -\ln \frac{2}{3} \approx 0.4055\)。
现在我们需要求解 \(T(t) = 40\) 时对应的 \(t\) 值:
解得 \(t = \frac{\ln 3}{0.4055} \approx 2.71\) 分钟。
因此,咖啡的温度降至 40°C 大约需要 2.71 分钟。
4.3.1 习题
- 一块铁块的初始温度为 100°C,放在 0°C 的冰水中。 1 分钟后,铁块的温度降至 50°C。 问:铁块的温度降至 10°C 需要多长时间?
- 推导牛顿冷却定律的解。
4.4 捕食者-猎物模型 -- 生态平衡¶
微分方程还可以用来描述生态系统中不同物种之间的相互作用。 一个经典的例子是 捕食者-猎物模型 (Lotka-Volterra 模型)。
这个模型描述了一个封闭的生态系统中,捕食者和猎物两个物种的数量变化规律。 假设:
- \(x(t)\) 表示猎物的数量,\(y(t)\) 表示捕食者的数量。
- 猎物的自然增长率与自身数量成正比,但会受到捕食者数量的负面影响。
- 捕食者的增长率与猎物数量成正比,但会受到自身数量的负面影响 (由于资源有限)。
根据这些假设,我们可以得到如下的微分方程组:
其中 \(a, b, c, d\) 都是正的常数。
这个方程组没有简单的解析解,但我们可以通过数值方法来求解它,或者对它进行定性分析。
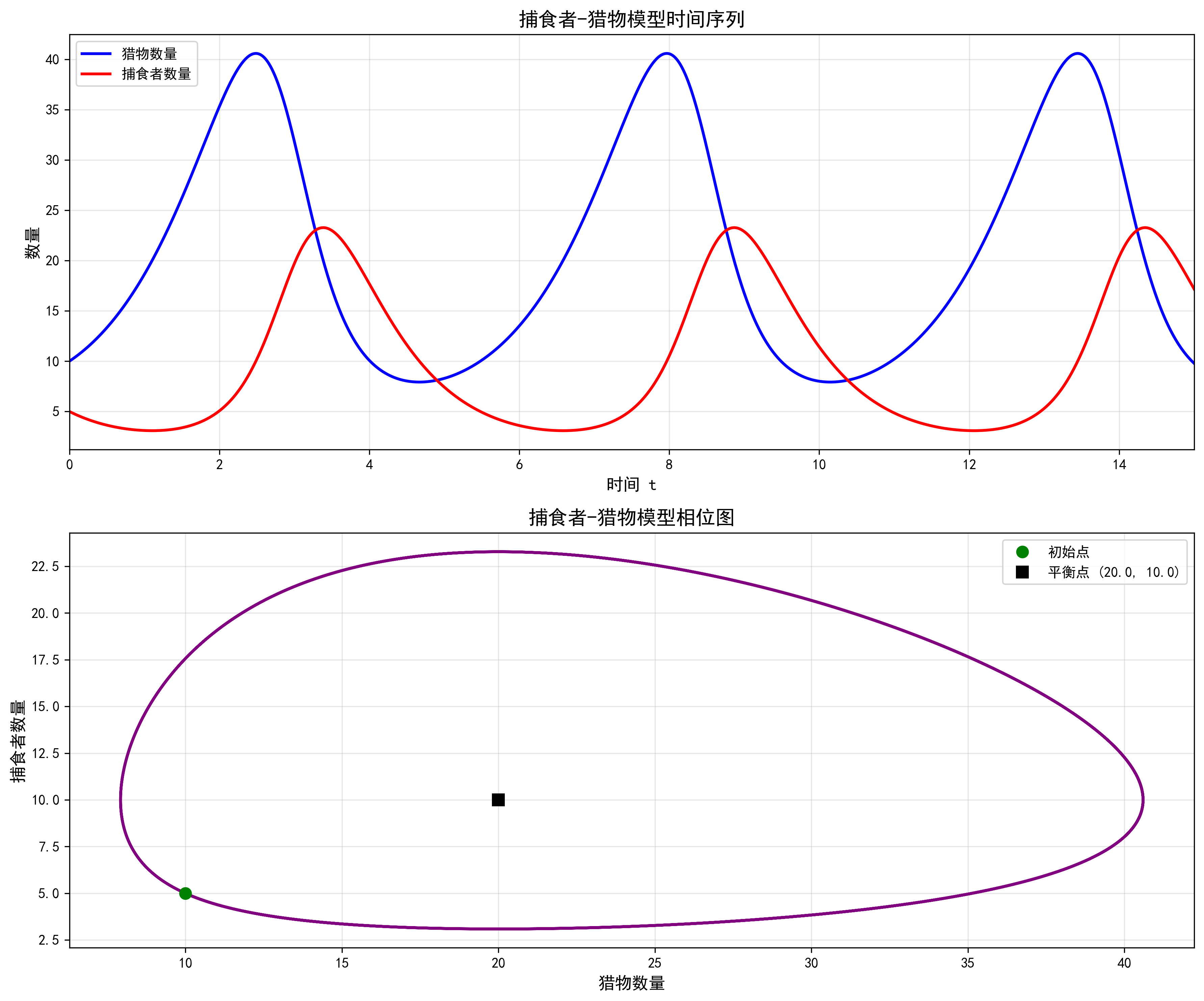
从图中我们可以看到,捕食者和猎物的数量都呈现出周期性振荡的现象。 这是因为当猎物数量增加时,捕食者由于食物充足而数量也随之增加;但当捕食者数量增加到一定程度后,猎物数量又会减少,从而导致捕食者数量也减少;而当捕食者数量减少后,猎物数量又会开始增加,如此循环往复。
捕食者-猎物模型是生态学中的一个基本模型,它揭示了生态系统中物种之间相互依存、相互制约的关系。
4.4.1 习题
- 解释捕食者-猎物模型中各个参数的含义。
- 如果考虑猎物数量的有限增长 (例如 Logistic 增长),捕食者-猎物模型应该如何修改?
- 请查阅资料,了解捕食者-猎物模型的其他应用,例如经济学中的竞争模型等。
4.5 电路模型 -- 电流的舞蹈¶
微分方程在电路分析中也扮演着重要的角色。
4.5.1 RC 电路
一个简单的 RC 电路由一个电阻 (R)、一个电容 (C) 和一个电源 (E) 串联而成。
设 \(q(t)\) 表示电容器上的电荷,\(i(t)\) 表示电路中的电流。 根据基尔霍夫定律,电路中的电压降之和等于电源电压,我们有:
由于电流 \(i(t) = \frac{dq}{dt}\),因此我们可以得到一个关于电荷 \(q(t)\) 的一阶线性微分方程:
如果电源电压 \(E(t)\) 是一个常数 \(E_0\),那么这个方程的解为:
其中 \(q_0 = q(0)\) 表示电容器的初始电荷。
电路中的电流为:
我们可以看到,电容器上的电荷将以指数形式趋近于 \(CE_0\),而电路中的电流则以指数形式衰减到 0。
4.5.2 RLC 电路
一个 RLC 电路由一个电阻 (R)、一个电感 (L)、一个电容 (C) 和一个电源 (E) 串联而成。
设 \(q(t)\) 表示电容器上的电荷,\(i(t)\) 表示电路中的电流。 根据基尔霍夫定律,我们有:
由于 \(i(t) = \frac{dq}{dt}\),因此我们可以得到一个关于电荷 \(q(t)\) 的二阶线性微分方程:
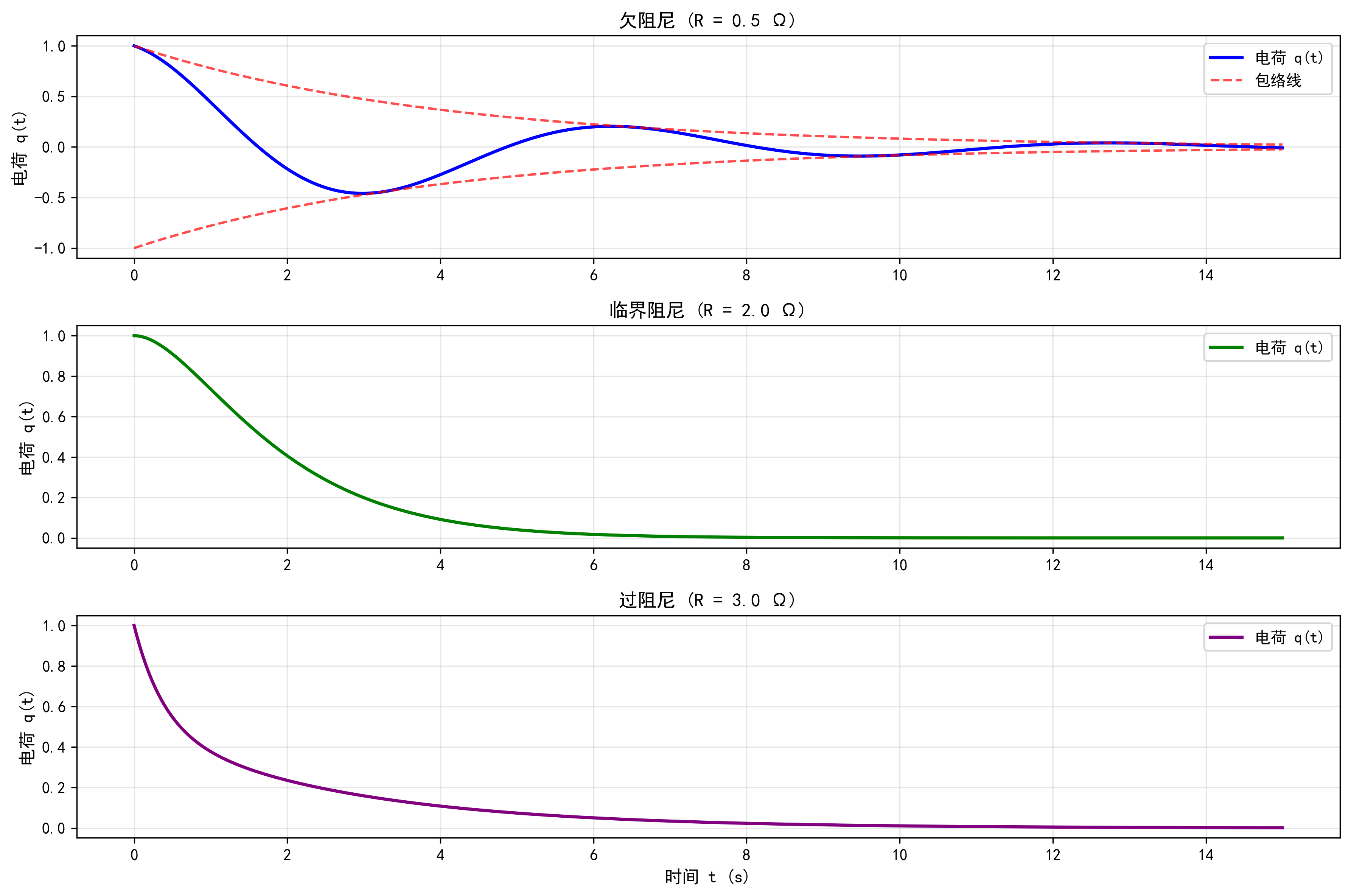
这个方程的解取决于电路的参数 \(R, L, C\) 以及电源电压 \(E(t)\) 的形式。
例如,如果电源电压 \(E(t) = 0\),且电路参数满足 \(R^2 - \frac{4L}{C} < 0\),那么电路的自由振荡将呈现阻尼振荡的形式。
4.5.3 习题
- 推导 RC 电路的解。
- 求解 RLC 电路的特征方程,并讨论电路参数对解的影响。
- 请查阅资料,了解 RLC 电路的其他应用,例如滤波器、振荡器等。
4.6 总结 -- 模型的魅力¶
通过以上几个例子,我们可以看到微分方程在各个领域都有着广泛的应用。 它可以帮助我们建立数学模型,描述各种现象的变化规律,并对未来的发展进行预测。
当然,建立一个好的数学模型并非易事。 我们需要根据实际情况,做出合理的假设,选择合适的数学工具,并对模型进行检验和修正。
微分方程只是众多数学工具中的一种,它也有自身的局限性。 但不可否认的是,微分方程是一种强大的工具,它为我们理解世界、改造世界提供了有力的武器。
希望通过本章的学习,大家能够感受到微分方程的魅力,并在未来的学习和工作中,学会运用微分方程来解决实际问题。
以上是 第四章:微分方程的应用 的主要内容。 考虑到篇幅,我只选取了几个具有代表性的例子进行了介绍。 实际上,微分方程的应用远不止这些,例如在化学反应动力学、自动控制、信号处理、图像处理、金融工程等等领域都有着重要的应用。